Understanding Huffman Coding: An Efficient Compression Algorithm

Why Do We Need Huffman Coding?

Huffman coding is a popular algorithm used for lossless data compression. It is named after David A. Huffman, who developed the algorithm while he was a Ph.D. student at MIT. The basic idea behind Huffman coding is to assign shorter codes to more frequent characters and longer codes to less frequent characters, thus reducing the overall size of the data.

Huffman tree

let’s start by exploring why Huffman coding is necessary. Imagine we have a simple text: “hello”. In traditional encoding schemes, every character is represented using a fixed number of bits. Let’s see how this works and why it can be inefficient.

What happens when we encode text using fixed-length encoding?

In ASCII encoding, each character is represented by 8 bits. Let’s encode the text “hello” using this scheme:

• h: 01101000
• e: 01100101
• l: 01101100
• o: 01101111

Combining these, we get:

01101000 01100101 01101100 01101100 01101111

Here, each character always uses 8 bits. This is straightforward, but it has a major drawback: it doesn’t consider how often each character appears.

The Problem with Fixed-Length Encoding

Let’s take a closer look at the character ‘l’ from our example:

• In ASCII, ‘l’ is encoded as 01101100 (8 bits).

If we use Huffman coding, we might find that ‘l’ could be represented with just 10 (2 bits), depending on its frequency. However, this raises a problem.

How can we distinguish between characters when their binary representations vary in length?

Imagine we have a binary sequence 10110010. How do we decode this? Is it:

• 10 1100 10 (where ‘10’ represents one character and ‘1100’ another)?
• Or 1 0110 010 (where ‘1’ represents one character and ‘0110’ another)?

Without knowing where each character starts and ends, decoding becomes challenging.

The Solution: Huffman Coding

Huffman coding provides a solution by creating a variable-length encoding system that is both efficient and unambiguous. Here’s how it works:

How does Huffman coding solve the problem of variable-length encoding?

1. Frequency Analysis:

• Determine the frequency of each character in the text.
• For example, in “hello”, ‘l’ appears 2 times, ‘h’, ‘e’, and ‘o’ appear once.

1. Build a Priority Queue:

• Create a min-heap where each node represents a character and its frequency.
• Combine nodes with the lowest frequencies to build a Huffman Tree.

1. Create Huffman Codes:

• Assign binary codes to characters based on their position in the tree.
• More frequent characters get shorter codes, and less frequent ones get longer codes.

Example:

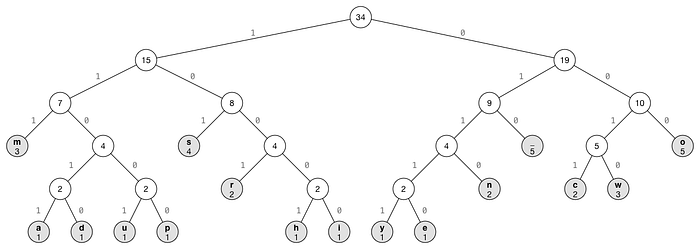
Suppose we build the Huffman Tree for “hello”:

• Characters: h, e, l, o
• Frequency Analysis:
• h: 1
• e: 1
• l: 2
• o: 1

Using Huffman coding, we might get the following codes:

• l: 0
• h: 10
• e: 110
• o: 111

Encoded Text Using Huffman Codes:

h: 10
e: 110
l: 0
o: 111

The encoded text for “hello” would be:

10 110 0 0 111

How does Huffman coding ensure that the encoded data can be correctly decoded?

Huffman coding guarantees that no code is a prefix of another. This property, known as prefix-free or prefix property, means that each code can be uniquely identified, making decoding straightforward and unambiguous.

Detailed Example in Python:

Here’s a Python implementation of Huffman coding with a step-by-step explanation:

import heapq
from collections import defaultdict, Counter

# Step 1: Frequency Analysis
def calculate_frequency(data):
    return Counter(data)

# Step 2: Build Priority Queue
def build_priority_queue(freq):
    heap = [[weight, [symbol, ""]] for symbol, weight in freq.items()]
    heapq.heapify(heap)
    return heap

# Step 3: Build Huffman Tree
def build_huffman_tree(heap):
    while len(heap) > 1:
        lo = heapq.heappop(heap)
        hi = heapq.heappop(heap)
        for pair in lo[1:]:
            pair[1] = '0' + pair[1]
        for pair in hi[1:]:
            pair[1] = '1' + pair[1]
        heapq.heappush(heap, [lo[0] + hi[0]] + lo[1:] + hi[1:])
    return heap[0]

# Step 4: Generate Huffman Codes
def generate_huffman_codes(huffman_tree):
    huff_codes = {}
    for symbol in huffman_tree[1:]:
        huff_codes[symbol[0]] = symbol[1]
    return huff_codes

# Example Usage
if __name__ == "__main__":
    data = "hello, this is an example"
    frequency = calculate_frequency(data)
    heap = build_priority_queue(frequency)
    huffman_tree = build_huffman_tree(heap)
    huffman_codes = generate_huffman_codes(huffman_tree)
    
    # Print Huffman Codes
    print("Character Codes:")
    for char, code in huffman_codes.items():
        print(f"{char}: {code}")
    
    # Encode Data
    encoded_data = "".join(huffman_codes[char] for char in data)
    print(f"\nEncoded Data: {encoded_data}")

    # Decode Data (Reverse mapping)
    reverse_huffman_codes = {v: k for k, v in huffman_codes.items()}
    decoded_data = ""
    temp = ""
    for bit in encoded_data:
        temp += bit
        if temp in reverse_huffman_codes:
            decoded_data += reverse_huffman_codes[temp]
            temp = ""
    print(f"\nDecoded Data: {decoded_data}")

Conclusion

Huffman coding addresses the inefficiencies of fixed-length encoding by using variable-length codes that are tailored to the frequency of characters. This not only reduces the overall size of the encoded data but also ensures that the encoded message can be uniquely and efficiently decoded. By understanding and implementing Huffman coding, we can achieve more efficient data compression and better utilize storage and transmission resources.

Reference: https://en.wikipedia.org/wiki/Huffman_coding